TDM 32100: Project Classification - Predicting Prescriptions for Ozempic Among Prescribers Using Logistic Regression
Project Objectives
In this project, you will build a Logistic Regression model to discover what features among prescribers increase the likelihood of them prescribing the drug Ozempic (also known as Semaglutide).
Dataset
-
/anvil/projects/tdm/data/CMS/diabetes_prescriber_data.csv`
Semaglutide (also known as Ozempic) has become more than a medication. It is a headline. It is the drug behind Ozempic and Wegovy, and lately it feels like everyone is talking about it. From celebrities on the red carpet to relatives at family gatherings, Semaglutide is in the spotlight.
This project looks at real prescription data to figure out what is driving the trend. Which types of prescribers are writing the most prescriptions? Is it more common among prescribers in some regions than others? And what makes Semaglutide different from other prescriptions?
We will start by loading and cleaning the data from CMS, exploring key features, and examining class balance. From there, we will dig into modeling and interpretation to better understand what kind of prescribers are behind this high profile drug.
About the Data
This dataset comes from the Centers for Medicare and Medicaid Services (CMS) and includes prescription-level records for diabetes medications. Each row represents a unique prescriber writing a prescription for a specific brand-name drug. Among these drugs is Semaglutide, the drug name behind Ozempic and Wegovy, medications originally approved for type 2 diabetes but now widely known for their off-label use in weight loss. This has made Semaglutide one of the most talked about and in demand drugs in the country.
Variables in the Data
Below are the columns you will be working with in this project:
| Column Name | Description |
|---|---|
|
Two-letter state abbreviation for the prescriber location. |
|
Detailed medical specialty of the prescriber (e.g. Family Practice, Endocrinology). |
|
Brand name of the prescribed drug (e.g. Ozempic). |
|
Generic name of the prescribed drug (e.g. Semaglutide). |
|
Total number of prescription claims for that drug by this prescriber. |
|
Approximate number of 30-day prescription fills. |
|
Total number of days of medication supplied. |
|
Total cost of the drug across all claims (in dollars). |
|
Total number of unique patients who received the drug. |
|
A simplified grouping of |
Questions
Class Distributions
Before we can analyze or model anything, we need to clean the data and add few new features (do some feature engineering).
One of the first things you will do is create a binary target variable to indicate whether a record involves Semaglutide. This kind of variable only takes on two values: 1 if the drug is Semaglutide, and 0 if it is not. In Python, you can create a binary variable using a boolean expression and then convert the result to integers using .astype(int).
For example:
df["Semaglutide_drug"] = (df["Gnrc_Name"] == "Semaglutide").astype(int)This creates a column where any row with Semaglutide is marked as 1, and all others are marked as 0. This will eventually serve as the outcome we try to predict.
Feature Engineering - Creating New Columns
Another important task we will perform is called feature engineering. Feature engineering is the process of transforming raw data into meaningful features that better represent the underlying problem to the predictive model. This includes creating, modifying, or grouping existing variables to enhance model performance or interpretability.
One simple but powerful example is creating a new column that provides more insight than the raw data alone. For instance, to understand how costly each prescription claim is, we can divide Tot_Drug_Cst (total drug cost) by Tot_Clms (total number of claims) to compute a new column called Cost_per_Claim:
diabetes_prescriber_data["Cost_per_Claim"] = diabetes_prescriber_data["Tot_Drug_Cst"] / diabetes_prescriber_data["Tot_Clms"]This gives us a per-claim cost that may be more meaningful for comparison across prescribers or regions.
Another useful technique is mapping existing values into broader categories. For example, individual state abbreviations in the Prscrbr_State_Abrvtn column can be mapped to broader U.S. Census regions. This can help us spot regional trends more easily than looking at each state individually:
state_region_map = {
"CT": "Northeast", "CA": "West", "TX": "South", ...
}
diabetes_prescriber_data["Prscrbr_State_Region"] = diabetes_prescriber_data["Prscrbr_State_Abrvtn"].map(state_region_map)By grouping states into regions, we reduce granularity while retaining useful geographic patterns, a valuable preprocessing step before modeling.
However, not all states in the dataset may appear in the dictionary. In those cases, .map() returns a missing value (NaN). To handle this, you can fill in those missing values with a default label like "Missing" using .fillna("Missing").
Value Counts
Finally, it is often useful to explore the distribution of values in a column. For example, how many rows fall into each region or how many are Semaglutide prescriptions. You can do this using .value_counts() for counts and .value_counts(normalize=True) for proportions.
These basic data preparation steps: binary indicators, feature engineering, mapping, and counting are critical in setting up a dataset for modeling. Once they are complete, you will have a clean, structured dataset that is ready for exploratory analysis.
1a. Read in the data and print the the first five rows of the dataset. Save the dataframe as diabetes_prescriber_data.
1b. Add a binary target column that equals 1 if Gnrc_Name is "Semaglutide" and 0 otherwise. Then, display the count of 1s and 0s in the column Semaglutide_drug.
Hint: Use a boolean comparison with .astype(int) to convert True/False values into 1s and 0s.
1c. Create a new column called Cost_per_Claim by dividing Tot_Drug_Cst by Tot_Clms. Then, print the first five rows of the following columns: Tot_Drug_Cst, Tot_Clms, and your new Cost_per_Claim` column to verify the calculation was performed correctly.
1d. Using the provided state_region_map dictionary below, create a new column named Prscrbr_State_Region that maps each Prscrbr_State_Abrvtn to its corresponding U.S. region. Any state abbreviation not found in the dictionary should be labeled as "Missing". After mapping, print the unique region values to verify your transformation.
Hints:
-
Use
.map()to apply the dictionary:df["new_col"] = df["existing_col"].map(mapping_dict) -
Use
.fillna("Missing")to replace any unmapped values. -
Use
.unique()to view the distinct region labels.
state_region_map = {
# Northeast
"CT": "Northeast", "ME": "Northeast", "MA": "Northeast", "NH": "Northeast", "NJ": "Northeast",
"NY": "Northeast", "PA": "Northeast", "RI": "Northeast", "VT": "Northeast",
# Midwest
"IL": "Midwest", "IN": "Midwest", "IA": "Midwest", "KS": "Midwest", "MI": "Midwest",
"MN": "Midwest", "MO": "Midwest", "NE": "Midwest", "ND": "Midwest", "OH": "Midwest",
"SD": "Midwest", "WI": "Midwest",
# Southb
"AL": "South", "AR": "South", "DE": "South", "DC": "South", "FL": "South", "GA": "South",
"KY": "South", "LA": "South", "MD": "South", "MS": "South", "NC": "South", "OK": "South",
"SC": "South", "TN": "South", "TX": "South", "VA": "South", "WV": "South",
# West
"AK": "West", "AZ": "West", "CA": "West", "CO": "West", "HI": "West", "ID": "West",
"MT": "West", "NV": "West", "NM": "West", "OR": "West", "UT": "West", "WA": "West", "WY": "West",
# Territories / Other
"PR": "Territory"
}1e. Print how many prescribers were assigned to each region, including "Missing".
Question 2: Exploratory Data Analysis (2 points)
Before we build any models, we need to take a step back and really get to know our data. This is the purpose of exploratory data analysis, or EDA. You can think of it like being a detective. You’re looking for patterns, inconsistencies, and clues that might help you understand how different variables relate to the outcome you’re trying to predict. In our case, that outcome is Semaglutide_drug, a column that tells us whether or not a prescription record involves the diabetes drug Semaglutide.
Each of the questions below helps uncover different aspects of the data structure and variability that may influence our model’s performance or interpretability.
Missing Values
We’ll start by checking for missing values in the numeric columns. This might seem minor, but it’s actually really important. If a feature is missing data for just a few rows, we might be able to fill it in or move on. But if half the values are missing, it could be a sign that the variable isn’t reliable for modeling.
To calculate the percentage of missing values, we can use the .isna() method to find missing entries, then apply .mean() to calculate the proportion of missing values in each column. Multiplying this by 100 gives us the percentage. You can also use .sum() if you want the raw count.
Group Statistics: Mean and Standard Deviation
Next, we’ll split the data into two groups: one where Semaglutide was prescribed and one where it wasn’t. Then we’ll calculate the mean (average) and standard deviation (a measure of spread) for key numeric features in each group.
This gives us insight into whether, for example, Semaglutide is associated with higher costs or larger patient counts. These statistics can help us start forming hypotheses, like whether prescribers who use Semaglutide tend to prescribe more 30-day fills or serve more patients.
To do this, we can use .groupby("Semaglutide_drug") followed by .agg(["mean", "std"]) on the numeric columns. This will create a side-by-side comparison table showing the average and variability for each group.
Correlation Between Numeric Variables
We’ll also explore how the numeric features relate to one another using correlation. Correlation is a measure that ranges from -1 to 1 and tells us how strongly two variables move together. A value close to 1 means they increase together, while -1 indicates that one tends to decrease as the other increases. A value near 0 suggests no clear relationship.
Heatmap Visualization
To visualize these relationships, we’ll use a heatmap. A heatmap is a color-coded grid where darker or brighter colors represent stronger relationships. This allows us to quickly see which variables are closely linked and potentially redundant.
To create the heatmap, we first use .corr() on the numeric columns to compute all pairwise correlations. Then we pass that matrix into sns.heatmap(), a Seaborn function that creates the visualization. By setting annot=True, we can print the correlation values directly on the plot, which makes it easier to interpret.
Geographic Patterns
Lastly, we’ll examine regional prescribing patterns. We want to know: do certain prescribers in certain regions prescribe Semaglutide more often? A good way to check this is with a count plot, which shows how many records come from each region — and whether Semaglutide was prescribed.
Using sns.countplot(), we can plot the number of prescribers in each Prscrbr_State_Region and split the bars by Semaglutide_drug using the hue parameter. This lets us compare across regions in one chart and spot any geographic trends in prescription behavior.
|
Learn more about count plots and how to use |
To explore correlations between numeric variables (like cost and total fills), we can use .corr() to compute pairwise relationships and sns.heatmap() to visualize them as a color-coded matrix.
|
See how to create heatmaps from correlation matrices:
Seaborn |
2a For the numeric columns ['Tot_30day_Fills', 'Tot_Day_Suply', 'Cost_per_Claim', 'Total_Patients'], print the percentage of missing values in the full dataset.
Hint: Create a list for numeric_cols. For example:
numeric_cols = ['Cost_per_claim', 'Tot_30day_Fills', 'Tot_Day_Suply', 'Total_Patients']2b. Group by Semaglutide_drug and calculate the mean and standard deviation of the numeric_cols. Then write 1–2 sentences on how the averages differ between the two classes and what that might suggest.
Hint: Use .groupby(target)[numeric_cols].agg(['mean', 'std']) to compute group-level summary statistics.
2c. Create a correlation matrix heatmap using the numeric columns to visualize how the variables are related. Then write 1–2 sentences on whether you think any numeric variables are strongly correlated with each other.
Hint:
-
Use
.corr()to get pairwise correlations of numeric_cols. -
Use
sns.heatmap()to visualize the correlation matrix. -
Set
annot=Truein.heatmap()if you’d like to display the correlation values directly in the plot.
2d. Create a bar plot showing the number of prescribers in each Prscrbr_State_Region, split by Semaglutide_drug. Then write 1-2 sentences on whether different regions prescribe Semaglutide more or less often.
Hint:
Use sns.countplot(data=…, x='Prscrbr_State_Region', hue='Semaglutide_drug')
Question 3: Train/Test Split and Data Preparation (2 points)
In predictive modeling, one of the first and most critical steps is to distinguish between your predictors (also known as features or independent variables) and your response (or target). The predictors are the pieces of information the model will use to make its decisions, while the response is the variable we wish to predict. In this context, we are interested in predicting whether a prescriber issued a prescription for Semaglutide which is a binary outcome that will form the basis of our classification model.
Splitting the Data
Models are not trained on entire datasets. Instead, we partition the data into multiple subsets to serve distinct roles in the model development process. The most common partitioning scheme involves three subsets:
-
Training data is what the model actually learns from. It’s used to find patterns and relationships between the features and the target.
-
Validation data helps us make decisions about the model such as choosing which features to keep or which settings (hyperparameters) work best. We use it to check how well it’s doing while we’re still building it.
-
Test data is completely held out until the very end. It gives us a final check to see how well the model is likely to perform on brand-new data it has never seen before.
|
In practice, it’s recommended to use cross-validation, which provides a more reliable estimate of a model’s performance by repeatedly splitting the data into training and validation sets and averaging the results. This helps reduce the variability that can come from a single random split. However, for the purpose of this project, we will not use cross-validation. Instead, we will perform a single random train/validation/test split using a fixed random seed. |
Stratified Sampling
One subtle but essential consideration is that we must maintain the distribution of the response variable, particularly in classification settings with imbalanced classes. To achieve this, we use stratified sampling, which ensures that the proportion of cases (e.g., Semaglutide = 1 vs. 0) remains consistent across the training, validation, and test sets. This avoids the model performing poorly simply because the subsets are not represented in the data.
Finally, it is good to inspect each of the resulting subsets. How many observations are in each split? Is the class balance preserved? These simple diagnostics are foundational checks that ensure the integrity of downstream modeling efforts which you will perform in the questions below.
3a. Use the provided code below to define your model’s features and create your X and y variables for modeling. Then, on your own, print the shape of X and y and display the first 5 rows of X to confirm everything looks correct.
# Define model features
model_features = ["Tot_30day_Fills", "Tot_Day_Suply", "Cost_per_claim", "Total_Patients", "Prscrbr_State_Region", "Prscrbr_Type_Grouped"]
# Define target and predictors
target_col = "Semaglutide_drug"
y = diabetes_prescriber_data[target_col]
X = diabetes_prescriber_data[model_features]3b. Split the dataset into 60% training, 20% validation, and 20% test using the code below. Then write 1–2 sentences, in your own words, explaining the purpose of each subset (train, validation, test).
from sklearn.model_selection import train_test_split
# Split off test set (20%)
X_train_val, X_test, y_train_val, y_test = train_test_split(
X, y, test_size=0.20, stratify=y, random_state=42
)
# Split remaining 80% into train (60%) and validation (20%)
X_train, X_val, y_train, y_val = train_test_split(
X_train_val, y_train_val, test_size=0.25, stratify=y_train_val, random_state=42
)3c. Print the number of rows and class proportions of the target variable Semaglutide_drug in each subset (train, val, and test).
Hint: Use len() to count rows and value_counts(normalize=True) for proportions.
Question 4 Preprocessing the Data (2 points)
Before we can fit our logistic regression model, we need to make sure our dataset is clean and formatted correctly. This stage, called preprocessing, ensures that our features are in a numerical format, have no missing values, are properly scaled, and are aligned across all datasets. Logistic regression, like many models, assumes that the data has been prepared in a certain way. If we skip these steps or do them incorrectly, our model may perform poorly or fail to train altogether.
These question will walk you through five key preprocessing steps, some of which have partially completed code to help guide you.
Handling Missing Values in Categorical Variables
Missing values can cause errors during modeling and interfere with scaling or encoding. For categorical columns like Prscrbr_State_Region and Prscrbr_Type_Grouped, we’ll fill in missing values with the string "Missing". This way, even rows with unknown data are retained and can be captured as their own category during encoding.
For numeric columns like Tot_30day_Fills, Tot_Day_Suply, Cost_per_Claim, and Total_Patients, we’ll fill missing values using the median from the training set. This is preferred over the mean because the median is less sensitive to outliers. You’ll use .fillna() to perform this replacement.
For one-hot encoded (binary) columns, we’ll fill missing values with 0. These columns represent the presence or absence of a category, so 0 safely indicates that the feature was not activated for that row.
One-Hot Encoding Categorical Variables
Machine learning models can’t interpret text categories directly. We convert them into numeric form using one-hot encoding, which creates a separate binary column for each unique category. For example, the column Prscrbr_State_Region might be transformed into:
-
Prscrbr_State_Region_Midwest -
Prscrbr_State_Region_South -
Prscrbr_State_Region_Northeast -
etc.
We use pd.get_dummies() to apply one-hot encoding. The option drop_first=True tells pandas to omit the first category — this prevents duplicate, which is especially important in models like logistic regression.
Why We Encode Train, Validation, and Test Separately
We always apply one-hot encoding to X_train first. That’s because we want the model to learn from the structure of the training data, including which categories exist. We then apply the same process to X_val and X_test — but here’s the tricky part:
-
These datasets may contain a different set of categories (some categories might be missing, or new ones might appear).
-
If we encoded all three together, we would risk leaking information from validation or test sets into training — which we want to avoid to ensure fair model evaluation.
To resolve this, we:
-
Encode each dataset separately using
pd.get_dummies(). -
Then use
.reindex(columns=encoded_columns, fill_value=0)onX_valandX_testto ensure their columns match the training set exactly — any missing columns will be added with `0`s.
This guarantees that the model sees inputs with the same structure at all stages (training, validation, testing), even if the underlying data varies.
Standardizing Numeric Features
Features that are on very different numeric scales can cause issues for models like logistic regression. For example, Tot_Day_Suply might be in the hundreds while Cost_per_Claim could be in the thousands. If we don’t scale them, the model might assign disproportionate importance to the larger features.
To address this, we use StandardScaler() from sklearn.preprocessing. This function subtracts the mean and divides by the standard deviation, resulting in a column with mean 0 and standard deviation 1. We fit the scaler on X_train[numeric_cols], and apply the transformation to X_train, X_val, and X_test.
Converting Boolean Columns
Some features may be stored as True/False. Most models, including logistic regression, expect numeric input. We use .astype(int) to convert all boolean columns into 1/0 format, which the model can interpret as binary indicators.
Final Structure Check
After all these steps, it’s important to verify that X_train, X_val, and X_test all have the same number and order of columns. This ensures the model receives a consistent input structure during training and evaluation.
|
Each of the steps in this question prepares your data for modeling. Some of the code has been provided for this section, make sure to fill in the missing pieces and reflect on why each step is needed. |
4a. Fill any missing values in the categorical variables with "Missing" across X_train, X_val, and X_test. Then, one-hot encode Prscrbr_State_Region and Prscrbr_Type_Grouped using X_train.
Note: Most of the code has been provided for you below. Your task is to complete the final line that performs one-hot encoding on the training set.
# Step 1: Fill missing values in categorical columns for all sets
categorical_cols = ['Prscrbr_State_Region', 'Prscrbr_Type_Grouped']
for df in [X_train, X_val, X_test]:
for col in categorical_cols:
df[col] = df[col].fillna("Missing")
# Step 2: One-hot encode only the training set
X_train = pd.get_dummies(..., drop_first=True) # For YOU to fill in4b. One-hot encode the same two variables, Prscrbr_State_Region and Prscrbr_Type_Grouped, in the validation and test sets. Then reindex X_val and X_test so their column structure matches X_train.
Note: The structure of the code is provided below. Your task is to complete the lines that apply one-hot encoding to the validation and test sets using pd.get_dummies(). This step is important to ensure that all datasets share the same set of columns before modeling.
X_test = pd.get_dummies(....., columns=categorical_cols, drop_first=True) # For YOU to fill in
X_val = pd.get_dummies(...., columns=categorical_cols, drop_first=True) # For YOU to fill in
# Save column names for alignment
# Aligning the columns across X_train, X_val, and X_test after one-hot encoding so
# all three datasets have the exact same structure
encoded_columns = X_train.columns
# Reindex to match training columns
# We are rearranging columns so that they match in order
X_test = X_test.reindex(columns=encoded_columns, fill_value=0)
X_val = X_val.reindex(columns=encoded_columns, fill_value=0)4c. Standardize the numeric features Tot_30day_Fills, Tot_Day_Suply, Cost_per_Claim, and Total_Patients across all datasets by filling in the missing lines of code below. Then write 1–2 sentences on what scaling is and why it is useful for logistic regression.
Note: Most of the code has been provided for you. Your task is to complete the missing pieces that handle missing values and apply standardization correctly.
import numpy as np
from sklearn.preprocessing import StandardScaler
# First identify numeric columns
numeric_cols = ['Tot_30day_Fills', 'Tot_Day_Suply', 'Cost_per_Claim', 'Total_Patients']
# These are the categorical variables that we one-hot encoded
one_hot_cols = [col for col in X_train.columns if col not in numeric_cols]
# Then fill missing values in numeric columns
for df in [X_train, X_val, X_test]:
df[numeric_cols] = df[numeric_cols].fillna( # For YOU to fill in: use medians from training data
________________
)
df[one_hot_cols] = df[one_hot_cols].fillna( # For YOU to fill in: what should missing one-hot values be?
________________
)
# Then standardize using StandardScaler()
scaler = StandardScaler()
X_train[numeric_cols] = scaler.fit_transform( # For YOU to fill in: what data do we fit on?
________________
)
X_val[numeric_cols] = scaler.transform( # For YOU to fill in
________________
)
X_test[numeric_cols] = scaler.transform( # For YOU to fill in
________________
)4d. Convert all boolean (True/False) columns in your training, validation, and test sets to integers (1/0).
Hint:
Use .select_dtypes(include='bool') to identify boolean columns.
Use .astype(int) to convert them.
4e. Confirm that X_train, X_val, and X_test all have the same number of columns. Then write 1-2 sentences on what one hot encoding is and why it was necessary to perform it seperately on the training, test and validation set.
Question 5 (2 points)
Logistic Regression and the Sigmoid Function
In binary classification problems, our goal is to predict the probability of a binary outcome: such as success/failure or 1/0.
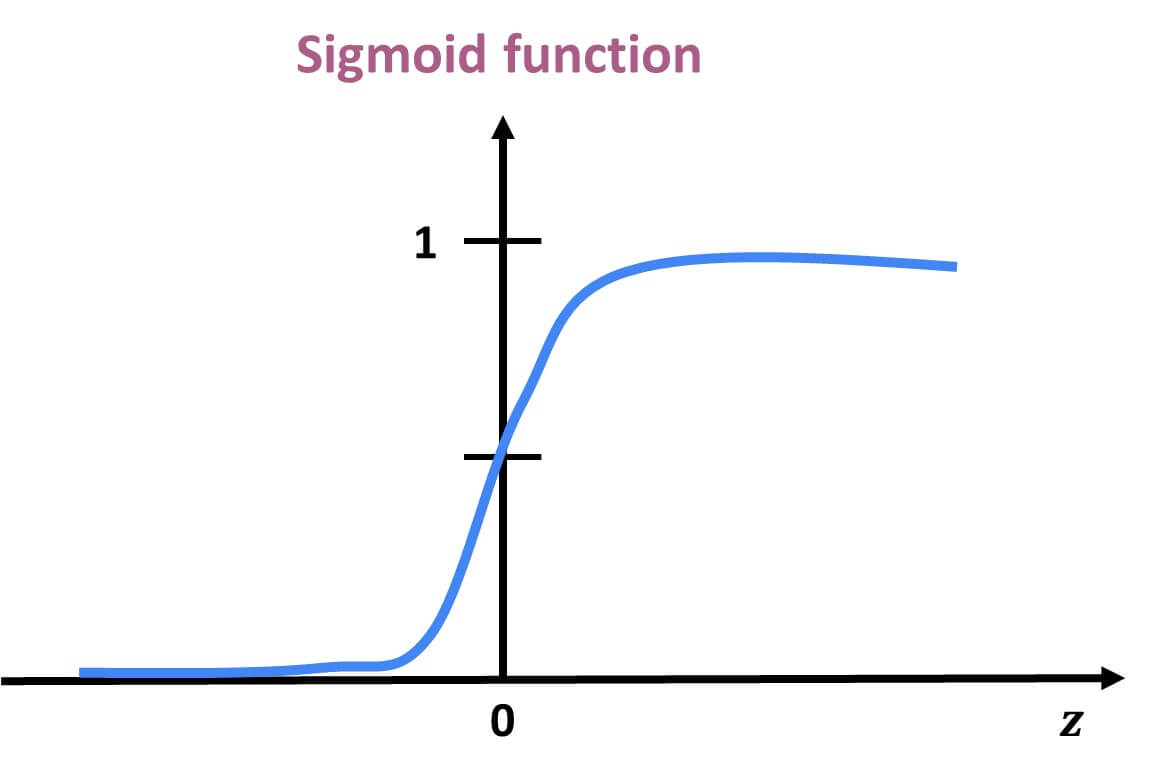
Unlike linear regression, which can produce any real number, logistic regression bounds the output between 0 and 1 by applying the sigmoid function.
This lets us model probabilities directly using the equation:
p = 1 / (1 + e^-(β₀ + β₁·X))
Where:
-
p is the predicted probability of success (e.g., winning)
-
β₀ is the intercept
-
β₁ is the coefficient for the input variable X
-
e is Euler’s number (approximately 2.718)
The result is an S-shaped curve that flattens near 0 and 1, making it ideal for modeling probabilities.
|
Why can’t this equation give probabilities outside of 0 to 1?
So the sigmoid function always produces values strictly between 0 and 1. |
Log Odds (Logit) Transformation
To make logistic regression behave like linear regression, we apply a transformation to the probability using log-odds, or the logit function:
log(p / (1 - p)) = β₀ + β₁·X
Where:
-
p / (1 - p) is called the odds — the probability of success divided by the probability of failure.
-
log(p / (1 - p)) is the log-odds, which maps probabilities (between 0 and 1) to the entire real number line.
|
If odds = 4, that means the event is 4 times more likely to happen than not. In other words, the probability of success is 4× greater than the probability of failure. |
Three Equivalent Forms of the Logistic Model
| Form | Expression |
|---|---|
Log-odds (logit) |
log(p / (1 - p)) = β₀ + β₁·X |
Odds |
p / (1 - p) = e^(β₀ + β₁·X) |
Probability (sigmoid) |
p = 1 / (1 + e^-(β₀ + β₁·X)) |
Each form is mathematically equivalent, and which one you use depends on the context:
-
Use log-odds when modeling or interpreting coefficients.
-
Use odds when communicating risk ratios.
-
Use probability when making predictions.
Key Features of the Logistic Curve
-
It always produces outputs between 0 and 1, making it ideal for probability modeling.
-
The log-odds transformation allows us to model the predictors in a linear way, just like in linear regression.
How to Interpret Coefficients
In a logistic regression model, each coefficient (β) represents the change in the log-odds of the outcome for a one-unit increase in the predictor, holding all else constant.
| Interpretation Type | What It Means |
|---|---|
Raw Coefficient (β) |
A one-unit increase in X increases the log-odds of the outcome by β. |
Exponentiated Coefficient (e^β) |
A one-unit increase in X multiplies the odds of the outcome by e^β. This is called the odds ratio. |
Odds Ratio > 1 |
The predictor increases the likelihood of the outcome. |
Odds Ratio < 1 |
The predictor decreases the likelihood of the outcome. |
Odds Ratio = 1 |
The predictor has no effect on the odds of the outcome. |
|
To interpret a coefficient as an odds ratio, you must exponentiate it: Odds Ratio = e^β This is especially helpful when explaining or interpreting the results in plain language! For example, if β = 0.75, then e^β ≈ 2.12, meaning a one-unit increase in that predictor makes the outcome about 2.1× more likely — or increases the odds by 112%. |
Checking Multicollinearity with VIF
Before fitting our model, we use Variance Inflation Factor (VIF) to check for multicollinearity:
VIF(Xᵢ) = 1 / (1 – R²ᵢ)
A VIF above 10 suggests the variable is highly collinear and may need to be removed.
Feature Selection with AIC and Forward Selection
To reduce the number of features, we use forward selection guided by Akaike Information Criterion (AIC):
AIC = 2·k – 2·log(L)
Where:
-
kis the number of parameters in the model -
Lis the likelihood of the model
A lower AIC indicates a better-fitting model with fewer parameters.
|
AIC is one of several possible criteria for feature selection. While we’re using AIC (Akaike Information Criterion) in this project, you could also use:
Each criterion has trade-offs. AIC is popular because it balances model fit and complexity, making it a solid choice when comparing logistic regression models. For consistency, we’ll use AIC throughout this project. |
Interpreting Model Coefficients with Odds Ratios
Once the model is fit, we convert coefficients into odds ratios to interpret them:
Odds Ratio = exp(β)
| Odds Ratio Value | Interpretation |
|---|---|
Greater than 1 |
Increases odds of prescribing Semaglutide |
Less than 1 |
Decreases odds of prescribing Semaglutide |
Equal to 1 |
No effect on the odds |
Evaluating Model Performance
Confusion Matrix
A confusion matrix compares the model’s predicted classes with the actual outcomes. It is used to calculate accuracy, precision, recall, and more.
| Predicted: No (0) | Predicted: Yes (1) | |
|---|---|---|
Actual: No (0) |
True Negative (TN) |
False Positive (FP) |
Actual: Yes (1) |
False Negative (FN) |
True Positive (TP) |
|
From the confusion matrix, we can compute key metrics:
| Metric | Formula |
|---|---|
Accuracy |
(TP + TN) / Total |
Precision |
TP / (TP + FP) |
Recall (Sensitivity) |
TP / (TP + FN) |
Specificity |
TN / (TN + FP) |
ROC Curve and AUC
A Receiver Operating Characteristic (ROC) curve plots the tradeoff between:
-
True Positive Rate (Recall)
-
False Positive Rate (1 – Specificity)
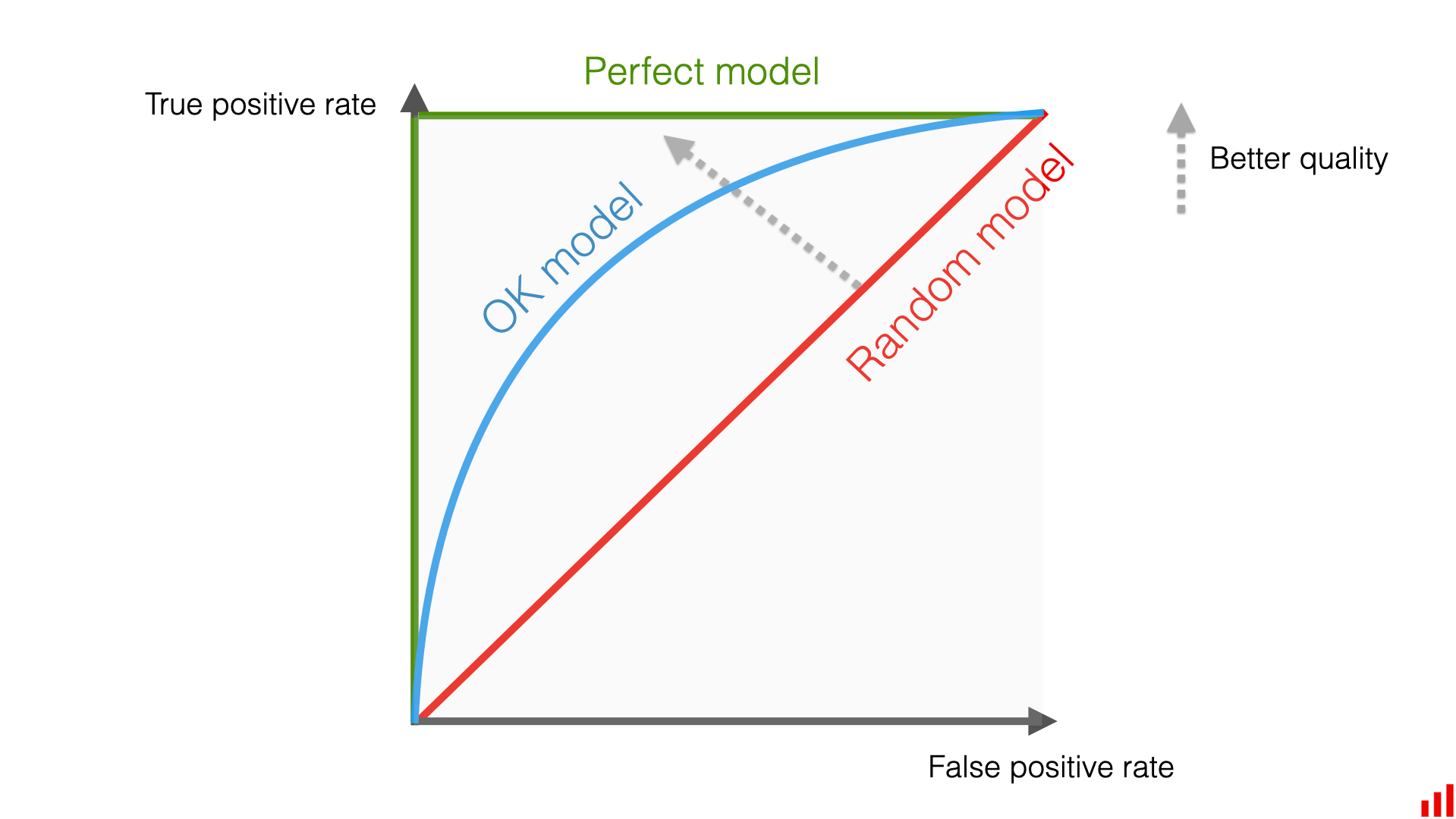
It shows how the model performs across all classification thresholds.
The Area Under the Curve (AUC) is a summary metric:
| AUC Score | Interpretation |
|---|---|
0.5 |
No better than random guessing |
0.7–0.8 |
Fair performance |
0.8–0.9 |
Strong performance |
1.0 |
Perfect classification |
|
AUC is threshold-independent — it evaluates how well the model ranks positive cases above negative ones, regardless of where we place the 0.5 decision boundary. |
You should compute and compare AUC scores for:
-
Training set
-
Validation set
-
Test set
This helps check for overfitting and ensure the model generalizes well.
Ready to Model
Now that you’ve reviewed the key concepts, proceed with training your logistic regression model and interpreting the results using this knowledge!
5a. Check for multicollinearity using VIF (Variance Inflation Factor) by completing the helper function provided below.
Your task is to complete the code below to calculate the VIF for each numeric column in your training data. Most of the function has been provided for you — just fill in the missing pieces to compute the VIF formula (stated above).
import pandas as pd
import numpy as np
from sklearn.linear_model import LinearRegression
def calculate_vif_manual(X):
vif_dict = {}
X = X.copy()
for feature in X.columns:
y = X[feature]
X_pred = X.drop(columns=feature)
model = LinearRegression().fit(X_pred, y)
r_squared = model.score(X_pred, y)
# Compute VIF
if r_squared == 1.0:
vif = np.inf
else:
# For YOU to fill in: implement the VIF formula below
vif = _____
vif_dict[feature] = vif
return pd.Series(vif_dict, name="VIF").sort_values(ascending=False)
# Prepare data
X_for_vif = X_train.select_dtypes(include=[np.number]).astype(float)
# Run VIF calculation
vif_values = calculate_vif_manual(X_for_vif)
print(vif_values)5b. Drop any variables with a VIF greater than 10, except for "Tot_Day_Suply", which you should keep regardless of its VIF value. Then write 1-2 sentences on what VIF is and why it is a neccessary step in model building for logistic regression.
The code below has already filtered out the appropriate features and created the list features_after_vif. Your task is to run this code and use it to subset the training data.
Note:
-
"Tot_Day_Suply"is an important feature, so we will keep it and remove the other two with a high VIF, even if its VIF exceeds the threshold. When multiple variables have high VIFs, you’d typically do additional testing to decide which to keep. For this project, we’ll keep"Tot_Day_Suply"because it’s interpretable and relevant, and remove the other two to reduce multicollinearity.
# Example after feature selection
features_after_vif = [
'Tot_Day_Suply',
'Cost_per_claim',
'Prscrbr_State_Region_South',
'Prscrbr_State_Region_West',
'Prscrbr_State_Region_Northeast',
'Prscrbr_Type_Grouped_Primary Care',
'Prscrbr_Type_Grouped_Dental',
'Prscrbr_Type_Grouped_Missing',
'Prscrbr_Type_Grouped_Dermatology/Ophthalmology',
'Prscrbr_Type_Grouped_Surgery',
'Prscrbr_Type_Grouped_Neuro/Psych',
'Prscrbr_Type_Grouped_Cardiology',
'Prscrbr_Type_Grouped_GI/Renal/Rheum',
'Prscrbr_Type_Grouped_Other',
'Prscrbr_Type_Grouped_Endocrinology',
"Prscrbr_Type_Grouped_Women's Health",
'Prscrbr_Type_Grouped_Oncology/Hematology',
'Prscrbr_State_Region_Territory',
'Prscrbr_Type_Grouped_Pulmonary/Critical Care',
'Prscrbr_Type_Grouped_Rehabilitation',
'Prscrbr_Type_Grouped_Anesthesia/Pain',
'Prscrbr_Type_Grouped_Palliative Care',
'Prscrbr_State_Region_Missing'
]
# Subset the training data
X_train = X_train[features_after_vif].copy()5c. Use forward selection to iteratively add features that result in the greatest reduction in AIC (Akaike Information Criterion). Then write 2–3 sentences explaining how forward selection works using AIC as the criterion and why this is an important step in model building for logistic regression.
Note: The function forward_selection() below has already been written for you. Your task is to run the code below and then write the 2–3 sentences explaining how forward selection works using AIC as the criterion and why this is an important step in model building for logistic regression.
import numpy as np
import statsmodels.api as sm
import statsmodels.tools.sm_exceptions as sme
import warnings
def forward_selection(X, y, aic_threshold=20, verbose=True):
np.seterr(over='raise', divide='raise', invalid='raise') # Raise numeric errors
included = []
current_score, best_new_score = np.inf, np.inf
while True:
changed = False
excluded = list(set(X.columns) - set(included))
scores_with_candidates = []
for new_col in excluded:
try:
with warnings.catch_warnings():
warnings.filterwarnings("ignore", category=sme.ConvergenceWarning)
model = sm.Logit(y, sm.add_constant(X[included + [new_col]])).fit(disp=0)
# Get summary statistics for stability check
summary = model.summary2().tables[1]
coef = summary.loc[new_col, 'Coef.']
std_err = summary.loc[new_col, 'Std.Err.']
# Heuristic thresholds to skip unstable models
if abs(coef) > 15 or std_err > 5:
if verbose:
print(f"Skipping {new_col} due to instability (coef={coef:.2f}, std_err={std_err:.2f})")
continue
aic = model.aic
scores_with_candidates.append((aic, new_col))
except (np.linalg.LinAlgError, FloatingPointError, KeyError):
if verbose:
print(f"Skipping {new_col} due to numerical error.")
continue
if not scores_with_candidates:
break
scores_with_candidates.sort()
best_new_score, best_candidate = scores_with_candidates[0]
if current_score - best_new_score >= aic_threshold:
included.append(best_candidate)
current_score = best_new_score
changed = True
if verbose:
print(f"Add {best_candidate:30} AIC = {best_new_score:.2f}")
if not changed:
break
return included
# Run the function
selected_features = forward_selection(X_train, y_train, verbose=False)
print("Selected features:", selected_features)5d. Use the provided code below to print model results and convert the logistic regression model coefficients into odds ratios. You only need to run the first cell of code, and fill in the blank in the second chunk where the odds ratios are calculated on final_model.params using np.exp() Then, write 1–2 sentences interpreting the results. In your explanation, briefly describe what an odds ratio represents in the context of logistic regression.
Note:
-
The first block of code fits a logistic regression model using the selected features to predict whether a provider prescribes Semaglutide. It prints a summary of the model, including coefficient estimates, p-values, and confidence intervals for each feature. It also outputs the AIC, which helps assess model quality — lower AIC values indicate a better-fitting model.
-
The second block of code will output three values for each feature: the odds ratio, which is calculated by exponentiating the model coefficients; the p-value, which comes directly from the model output and tells us if the feature is statistically significant; and the direction, which summarizes whether the feature increases, decreases, or has no effect on the odds of the outcome (whether or not a prescriber wil prescribe the drug Semaglutide). Make sure to fill in the blank in the this second block of code to calculate odd ratios.
import statsmodels.api as sm
import warnings
warnings.filterwarnings("ignore")
# Final feature matrix and target
X_train_final = sm.add_constant(X_train[selected_features]).astype(float)
final_model = sm.Logit(y_train, X_train_final).fit()
# Display model summary and AIC
print(final_model.summary())
print(f"\nFinal AIC: {final_model.aic}")import numpy as np
import pandas as pd
# Calculate odds ratios for final_model.params
odds_ratio_values = np.exp(...) # For YOU to fill in
# Build odds ratio DataFrame
odds_ratios = pd.DataFrame({
"Odds Ratio": odds_ratio_values,
"P-value": final_model.pvalues
})
# Add Direction column
odds_ratios["Direction"] = odds_ratios["Odds Ratio"].apply(
lambda x: "Increases Odds" if x > 1 else ("Decreases Odds" if x < 1 else "No Effect")
)
# Round and sort
odds_ratios = odds_ratios.round({"Odds Ratio": 3, "P-value": 4})
odds_ratios = odds_ratios.sort_values("Odds Ratio", ascending=False)
odds_ratios.reset_index().rename(columns={"index": "Feature"})5e. Run the code below to create and print confusion matrices for the training, validation, and test sets using the code below. Fill in the missing line that converts the output into a labeled DataFrame. Write 1–2 sentences to interpret the results of the confusion matrix and write whether there are any signs of overfitting.
import warnings
warnings.filterwarnings("ignore")
import statsmodels.api as sm
import pandas as pd
import numpy as np
from sklearn.metrics import classification_report, roc_auc_score, confusion_matrix, roc_curve
import matplotlib.pyplot as plt
# Step 1: Final feature matrix for training
X_train_final = sm.add_constant(X_train[selected_features]).astype(float)
final_model = sm.Logit(y_train, X_train_final).fit(disp=0)
# Step 2: Prepare validation and test sets
X_val_final = sm.add_constant(X_val[selected_features]).astype(float)
X_test_final = sm.add_constant(X_test[selected_features]).astype(float)
# Align columns
X_val_final = X_val_final[X_train_final.columns]
X_test_final = X_test_final[X_train_final.columns]
# Step 3: Predict probabilities
train_preds = final_model.predict(X_train_final)
val_preds = final_model.predict(X_val_final)
test_preds = final_model.predict(X_test_final)
# Step 4: Convert to binary labels
train_pred_labels = (train_preds >= 0.5).astype(int)
val_pred_labels = (val_preds >= 0.5).astype(int)
test_pred_labels = (test_preds >= 0.5).astype(int)
# Step 7: Confusion matrices
def display_confusion_matrix(y_true, y_pred, label):
cm = confusion_matrix(y_true, y_pred)
df_cm = pd.DataFrame(cm, index=["Actual 0", "Actual 1"], columns=["Predicted 0", "Predicted 1"])
print(f"\n{label} Confusion Matrix:")
print(df_cm)
display_confusion_matrix(y_train, train_pred_labels, "Train")
display_confusion_matrix(y_val, val_pred_labels, "Validation")
display_confusion_matrix(y_test, test_pred_labels, "Test")5f. Plot ROC curves and print AUC scores for the train, validation, and test sets using the code below. Then, write 1–3 sentences interpreting what this tells you about your model’s performance and generalizability of the model.
# Step 8: ROC Curves
def plot_roc(y_true, y_proba, label):
fpr, tpr, _ = roc_curve(y_true, y_proba)
auc_score = roc_auc_score(y_true, y_proba)
plt.plot(fpr, tpr, label=f"{label} (AUC = {auc_score:.2f})")
plt.figure(figsize=(8, 6))
plot_roc(y_train, train_preds, "Train")
plot_roc(y_val, val_preds, "Validation")
plot_roc(y_test, test_preds, "Test")
plt.plot([0, 1], [0, 1], 'k--', label="Random Classifier")
plt.xlabel("False Positive Rate")
plt.ylabel("True Positive Rate")
plt.title("ROC Curves - Train, Validation, and Test")
plt.legend(loc="lower right")
plt.grid(True)
plt.show()
# Step 5: AUC scores
print("Train AUC:", roc_auc_score(y_train, train_preds))
print("Validation AUC:", roc_auc_score(y_val, val_preds))
print("Test AUC:", roc_auc_score(y_test, test_preds))Question 6: Make Predictions on New Prescribers (2 points)
Now that you’ve trained your final model, let’s use it to predict how likely new prescribers are to prescribe Semaglutide.
The Sigmoid Function and Likelihood in Logistic Regression (Semaglutide Example)
Let’s say we have a prescriber with the following characteristics:
-
22 total 30-day fills
-
$450 per claim
-
Practices in the South
-
Internal Medicine specialist
Using the sigmoid function, the model calculates p = 0.83, meaning there’s an 83% chance this provider prescribes Semaglutide.
So:
-
If this provider did prescribe Semaglutide, their likelihood = 0.83
-
If this provider did not prescribe Semaglutide, their likelihood = 1 – 0.83 = 0.17
Maximum Likelihood Estimation (MLE)
To train the model, we use maximum likelihood estimation.
This means we:
-
Calculate the likelihood for each prescriber in the data (based on whether or not they prescribed Semaglutide).
-
Multiply all the individual likelihoods together to get a total likelihood.
-
Adjust the coefficients (β₀, β₁, etc.) to maximize that total likelihood.
Example:
If the model predicts:
-
Prescriber A: p = 0.75, and they did prescribe → likelihood = 0.75
-
Prescriber B: p = 0.20, and they did not prescribe → likelihood = 0.80
-
Prescriber C: p = 0.55, and they did prescribe → likelihood = 0.55
Then the total likelihood is:
Likelihood = 0.75 × 0.80 × 0.55
We want to find the coefficients that maximize this product across all rows in the dataset.
|
Logistic regression finds the coefficients that maximize the likelihood of the observed outcomes. That’s how we “fit” the model and it’s also how we estimate the best values for the βs in the sigmoid equation. |
6a. Select 20 random prescribers from X_test using the .sample() function and save it as sample_prescribers. Make sure to set n=20 and random_state=123 to ensure reproducibility.
6b. Run the code below to predict the probability that each prescriber in the sample will prescribe Semaglutide using the final_model. Then, on your own, print the top 5 rows.
# Add constant and align columns
sample_prescribers_final = sm.add_constant(sample_prescribers[selected_features])
sample_prescribers_final = sample_prescribers_final[final_model.params.index]
# Predict probabilities
sample_preds = final_model.predict(sample_prescribers_final)
# Create new DataFrame with probabilities
scored_sample = sample_prescribers.copy()
scored_sample["Predicted_Probability"] = sample_preds6c. Write 1–2 sentences interpreting the results. What do the top-scoring prescribers have in common? Does anything surprise you?
Submitting your Work
Once you have completed the questions, save your Jupyter notebook. You can then download the notebook and submit it to Gradescope.
-
firstname_lastname_project1.ipynb
|
You must double check your You will not receive full credit if your |